E~h^2(E는 error)
logE~ 2logh~ -2logN
x=logN, y=logE에 대한 그래프에서 기울기(Least Square Fit)
scipy packages, curvefit 사용해서 기울기 구하기
rectangular method, trapezoidal method, simpon rule, simpons rule 3/8 비
error: MAE(Mean Absolute Error)
선형 회귀 시켜서 기울기를 비교해보자

import numpy as np
import matplotlib.pyplot as plt
def rectangular(f, x0, x1, N=100):
x=x0
h=(x1-x0)/N
s=0.
for i in range(N):
s+=f(x+h/2)*h
x+=h
return s
def trapezoidal(f, x0, x1, N=100):
x=x0
h=(x1-x0)/N
s=0.
for i in range(N):
s+=(f(x)+f(x+h))*h/2
x+=h
return s
def simpson_13(f, x0, x1, N=100):
if N%2==0:
N+=1
x=np.linspace(x0, x1, N)
h=x[1]-x[0]
s=0.
for i in range(0, N-2, 2):
s+=(f(x[i+2])+4*f(x[i+1])+f(x[i]))*h/3
return s
def simpson_38(f, x0, x1, N=100):
if N%3==0:
N+=1
elif N%3==2:
N+=2
x=np.linspace(x0, x1, N)
h=x[1]-x[0]
s=0.
for i in range(0, N-3, 3):
s+=(f(x[i])+3*f(x[i+1])+3*f(x[i+2])+f(x[i+3]))*3*h/8
return s
# MSE에서의 선형 회귀 기울기
def gradient_MSE(x, y):
_x=np.array(x); _y=np.array(y)
mx=_x.mean(); my=_y.mean()
dd=(_x-mx)*(_y-my)
dr=(_x-mx)**2
return dd.sum()/dr.sum()
if __name__=="__main__":
def sin(x):
return np.sin(x)
# real integral for sin(x) [0, pi]
REAL_VAL=2
x_range=[0, np.pi]
rect_list=[]
trap_list=[]
sim13_list=[]
sim38_list=[]
N=np.linspace(10, 1e3, 10, dtype=int)
for n in N:
rect_list.append(rectangular(sin, x_range[0], x_range[1], n))
trap_list.append(trapezoidal(sin, x_range[0], x_range[1], n))
sim13_list.append(simpson_13(sin, x_range[0], x_range[1], n))
sim38_list.append(simpson_38(sin, x_range[0], x_range[1], n))
rect_err=abs(np.array(rect_list)-REAL_VAL)
trap_err=abs(np.array(trap_list)-REAL_VAL)
sim13_err=abs(np.array(sim13_list)-REAL_VAL)
sim38_err=abs(np.array(sim38_list)-REAL_VAL)
plt.plot(N, rect_err, label="Rectangular method")
plt.plot(N, trap_err, label="Trapezoidal method")
plt.plot(N, sim13_err, label="Simpson 1/3 Rule")
plt.plot(N, sim38_err, label="Simpson 3/8 Rule")
plt.legend()
plt.xscale("log")
plt.yscale("log")
plt.xlabel(r"$\log N$")
plt.ylabel(r"$\log(error[AE])$")
plt.title(r"$\int_{0}^{\pi} \sin(x)\,dx$ Absoulute Error")
log_rect_err=np.log(rect_err)
log_trap_err=np.log(trap_err)
log_sim13_err=np.log(sim13_err)
log_sim38_err=np.log(sim38_err)
log_N=np.log(N)
ra=gradient_MSE(log_N, log_rect_err)
rt=gradient_MSE(log_N, log_trap_err)
rs13=gradient_MSE(log_N, log_sim13_err)
rs38=gradient_MSE(log_N, log_sim38_err)
plt.text(N[0], rect_err[0], ra)
plt.text(3*N[0], trap_err[1], rt)
plt.text(5*N[0], sim13_err[2], rs13)
plt.text(N[2], sim38_err[3], rs38)
plt.show()
RA: -2.0005813963570733
RT: -2.0003323515392015
RS13: -4.002332380371419
RS38: -4.090331895197583
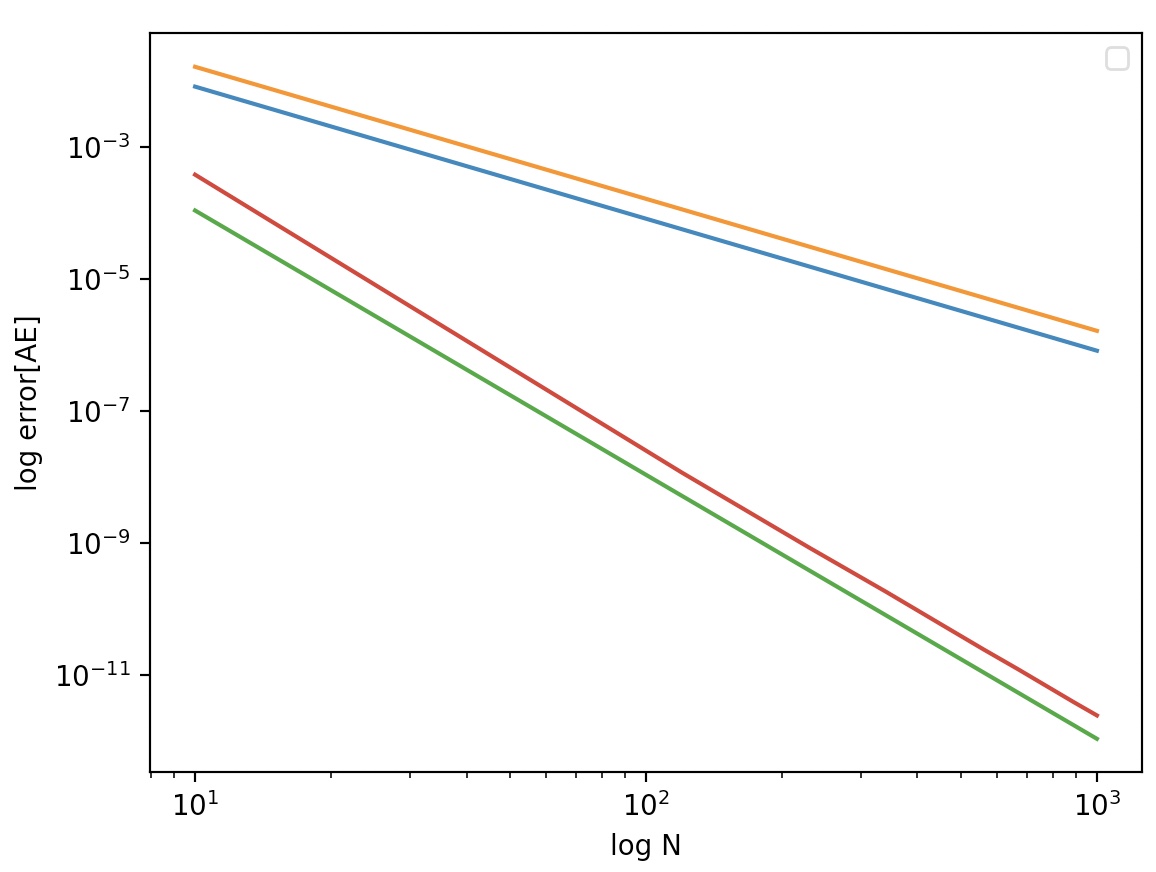
N[1, 1e4] 까지는 일정하게 감소
RA: -2.0003440163061526
RT: -2.0001820458613953
RS13: -2.6467514860948076
RS38: -2.779609588555073
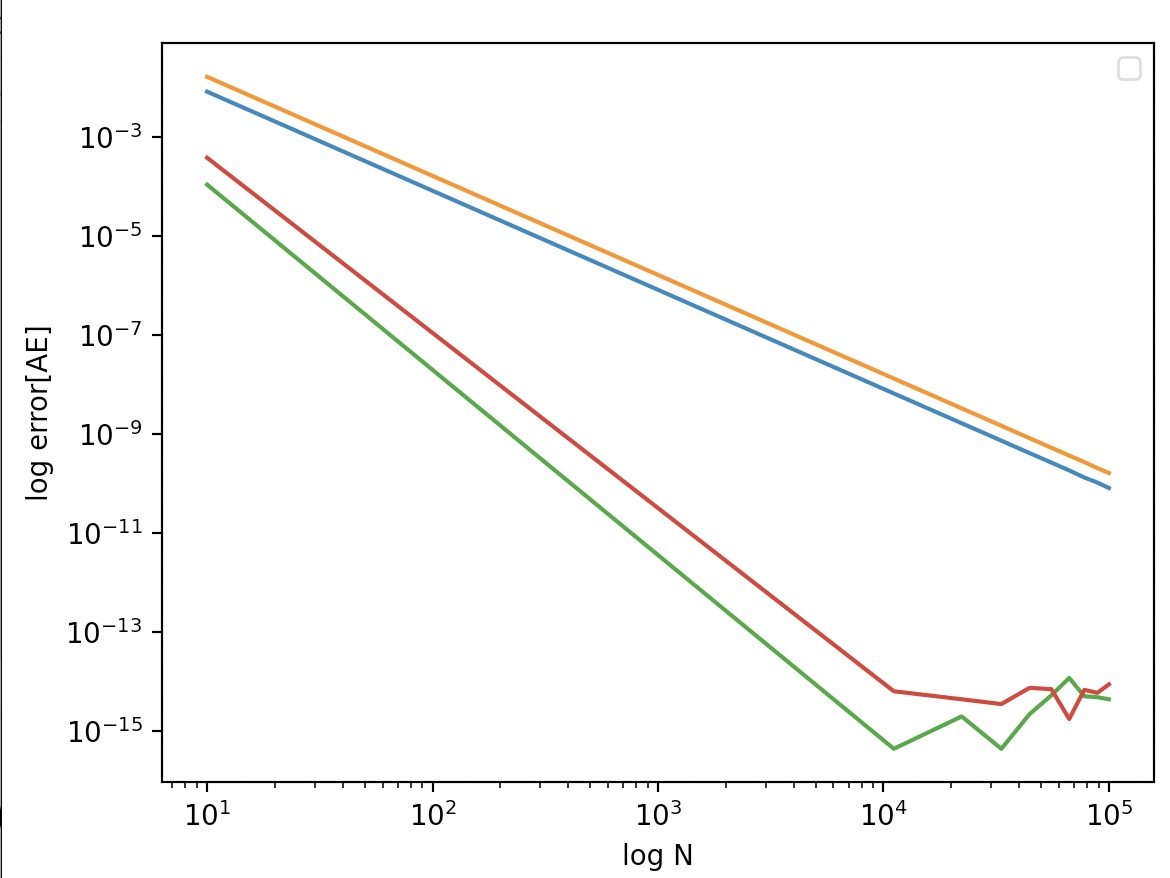
N[1e4-] 변동이 생기기 시작함